Αlice in wonderland / 1

****

Aν μπορείς να δεις το 1 , τότε μπορείς να δεις και τo 1+0i

Ένας μιγαδικός αριθμός z είναι ένας αριθμός που αποτελείται από το πραγματικό και από το φανταστικό του κομμάτι και γράφεται ως z=a+bi

Ορίζουμε ως Re(z)=a , δηλαδή πραγματικό κομμάτι του z &

Im(z)=b και φανταστικό κομμάτι του z

όπου τα a,b είναι πραγματικοί αριθμοί.

Φυσική συνέπεια, κάθε πραγματικός αριθμός μπορεί να γραφτεί στη μορφή αυτή, αρκεί το φανταστικό του τμήμα να είναι ίσο με 0, δηλαδή είτε γράψουμε 3 είτε γράψουμε 3+0i είναι ακριβώς το ίδιο

Η ιστορία των μαθηματικών είναι γεμάτη επεκτάσεις, για να λυθεί η 3x+1=0 , η επέκταση έγινε στο Ζ , και πρσοτέθηκαν οι αρνητικοί αριθμοί

Για να μπορέσει να λυθεί η x^^2 + 1 =0 ,η επέκταση γίνεται σε ένα υπερσύνολο που περιλαμβάνει και τους φανταστικούς αριθμούς , το σύνολο των μιγαδικών αριθμών, C

Το  i είναι μια κατεξοχήν ευρωπαϊκή σύλληψη που χρωστά τη γέννησή της στον Ιταλό Μαθηματικό Gerolamo Cardano όταν προσπαθούσε να επιλύσει την πολυωνυμική εξίσωση 3ου βαθμού

Στην προσπάθεια αυτή ο Cardano χρησιμοποίησε την √-1 ονομάζοντάς την i , δημιουργώντας με τη σειρά του μια ομάδα αριθμών που τους έδωσε την ονομασία “fictitious”

Οι πολυωνυμικές εξισώσεις τρίτου βαθμού είναι της μορφής 2x^3- -x² –5x+4=0. Στην προσπάθειά μας να βρούμε λύσεις σε τέτοιες εξισώσεις προσπαθούμε να καταλήξουμε σε γνωστές εξισώσεις χρησιμοποιώντας το θεώρημα που λέει, ότι οι ακεραίες λύσεις μια πολυωνυμικής εξίσωσης θα βρίσκονται ανάμεσα στους διαιρέτες τους σταθερού της όρου ( στη συγκεκριμένη περίπτωση είναι το -1 )

Αν βρούμε μια τέτοια ρίζα , τότε με το σχήμα του Horner ή με κανονική διαίρεση πολυωνύμων, επαναδιατυπώνουμε την εξίσωση ως γινόμενο του παράγοντα που την διαιρεί και ενός τριωνύμου ( δευτεροβάθμιας εξίσωσης ).

Εκεί , αποφασίζουμε αν η δευτεροβάθμια είναι in casus irreducibilis ανάλογα με την διακρίνουσα του τριωνύμου ( της δευτεροβάθμιας ).

Αν η διακρίνουσα D >0 τότε η δευτεροβάθμια έχει δύο ρίζες πραγματικές και άνισες

Αν D=0, η δευτεροβάθμια έχει μια ρίζα διπλή γιατί είναι τέλειο τετράγωνο

και αν D<0 η δευτεροβάθμια έχει μιγαδικές ρίζες της μορφής a+bi

Στο δικό μας παράδειγμα η 2x^3- -x² –5x+4= ( x-1)(2x²+x-4) και ο αν οι ρίζες μας θα είναι μιγαδικές ή πραγματικές θα μας το δώσει η D=(+1)²-4*2*(-4)=1+32=33>0 ( όπου

-1 ο συντελεστής του x, +2 του x² και -4 ο σταθερός όρος , D=β²-4αγ

Εδώ οι ρίζες είναι και οι τρεις πραγματικές. Αν η D<0 αποφασίζουμε εμείς για το αν θα προχωρήσουμε στην εύρεση μιγαδικών ριζών, ανάλογα με τη χρήση που σκοπεύουμε να τους κάνουμε στη συνέχεια.

Σύφωνα με τους Cardano & Tartaglia , η τεχνική αυτή συμφωνεί με το θεμελιώδες θεώρημα της Άλγεβρας στη διατύπωσή του ότι με τη χρήση των φανταστικών αριθμών κάθε πολυωνυμική εξίσωση τρίτου βαθμού έχει 3 ρίζες οπωσδήποτε.

Ο επόμενος που ασχολήθηκε μαζί τους ήταν ο Rafael Bombelli που όρισε το πώς γίνονται οι 4 πράξεις των μιγαδικών και την ολοκλήρωση έκανε ο William Hamilton απεικονίζοντάς τους στο χώρο

Πριν τους κατανοήσουμε καλύτερα γιατί πραγματικά οι πράξεις τους έχουν ενδιαφέρον, ας πούμε ότι η χρήση τους είναι ιδιαίτερη στους μηχανικούς, στον ηλεκτρομαγνητισμό, στα εφαρμοσμένα μαθηματικά και στη θεωρία του χάους και όπου στη μαθηματική βιβλιογραφία συναντάτε τη λέξη complex σημαίνει ότι για να γίνει θεμελίωση έχει γίνει χρήση μιγαδικών

Πώς γίνονται οι τέσσερεις πράξεις;

΄Έστω λοιπόν ότι έχουμε τους z=a+bi και w=x+yi

Για να ορίσουμε z+w θα έχουμε : ( a+bi)+(x+yi) = ( a+x)+i(b+y)

και z-w = (a+bi)-(x+yi)=(a-x)+(b-y)i

Δηλαδή αν z= 4+3i & w= 5-6i, z+w=(4+5)+(3-6)i => z+w=9-3i &

z-w=(4+3i)-(5-6i)=(4-5)+(3-(-6))i => z-w = -1+9i

δηλαδή z+w=Re(z)+Re(w) +i(Im(z)+Im(w)) & z-w=(Re(z)-Re(w))-((Im(z)-Im(w))i

Ο πολλαπλασιασμός έχει μια σχετική πολυπλοκότητα , γίνεται με επιμεριστική ιδιότητα και θέλει προσοχή γιατί το I υψώνεται στο τετράγωνο και δίνει ένα απροσδόκητο -1 που μπερδεύει στην αρχή δεδομένου ότι συνειδησιακά έχουμε συνδέσει τα τετράγωνα με θετικές ποσότητες ( και όπως έλεγε και ένας καθηγητής μου στο πολυτεχνείο, όποιος ξεπέρασε εύκολα αυτό το φράγμα του τετράγωνου με το θετικό δηλαδή, βρέθηκε σε αυτά εδώ τα έδρανα και η ψυχική του υγεία τίθεται υπό αμφισβήτηση )

Για να μην το κουράζουμε και πολύ, zw = ( a+bi)(x+yi)= ax – by +(ay+bx)i

Όσον αφορά τη διαίρεση δύο μιγαδικών, εδώ θα σταθούμε λίγο και θα συζητήσουμε το θέμα του συζυγούς μιγαδικού . Για κάθε μιγαδικό αριθμό z = a+bi, υπάρχει ο συζυγής του που είναι ο

z=a-bi και συμβολίζεται με μια παύλα πάνω από το z

Η φιλοσοφία είναι ότι στα μαθηματικά στα πηλίκα δεν θέλουμε στους παρονομαστές τετραγωνικές ρίζες και μιγαδικούς, οπότε γίνεται ένας πολλαπλασιασμός μεταξύ συζυγών και η διαίρεση ανάμεσα στο z και το w παίρνει τη μορφή , z/w = ( a+bi)/ (x+yi) = (a+bi)(x-yi)/(x+yi)(x-yi) =

(ax+by)/(x²+y²) + i((ay+bx)/(x²+y²))

Στο επόμενο και πάλι μιγαδικοί, γιατί πραγματικά παρουσιάζουν μεγάλο ενδιαφέρον

Και ένα κινέζικο πρόβλημα με μεγάλη ιστορία/2

Στο προηγούμενο ποστ ξεκινήσαμε από τα σιτάρια, φτάσαμε μέχρι τους επαυξημένους πίνακες με ορίζουσα ίση με το μηδέν για να διαπιστώσουμε αν το σύστημα έχει λύση, εξηγήσαμε τη φυσική σημασία των πρωτοβαθμίων εξισώσεων γεωμετρικά και σταματήσαμε μπροστά στο πρώτο όνομα που ξανα-ασχολήθηκε μαζί τους : τον Leibniz που μπορεί μεν να ήταν ο πρώτος αλλά δεν ήταν ο μόνος που ασχολήθηκε με το θέμα.

Το 1729, ο MacLaurin ( για όσους ξέρουν, θα θυμίσω τα αθροίσματα του McLaurin ) χρησιμοποίησε όχι πίνακες αλλά ορίζουσες για την επίλυση των συστημάτων, όμως η μέθοδος αυτή έμεινε γνωστή με το όνομα του G. Cramer ( εξ’ ου και ο  όρος ‘συστήματα του Cramer ‘) ο οποίος την παρουσίασε στο βιβλίο του  «Εισαγωγή στην ανάλυση των αλγεβρικών καμπύλων γραμμών» ( 1750 )

Το πρόβλημα του Cramer ξεκίνησε όταν θέλησε να προσδιορίσει μια καμπύλη που διέρχεται από 5 γνωστά σημεία και έχει εξίσωση της μορφής

A+By+Cx+Dy^2+Exy+x^2 = 0

οπότε αναγκαστικά κατέληξε σε ένα γραμμικό σύστημα 5 εξισώσεων με αγνώστους τα A,B,C,D,E . Αφήνει κατά μέρος την αρχική ιδέα και αρχίζει να περιγράφει  μια μέθοδο υπολογισμού των αγνώστων με κατασκευή κλασμάτων , που έχουν κοινό παρονομαστή και αριθμητές που προσδιορίζονται από τους συντελεστές τους συστήματος  σύμφωνα με γενικούς κανόνες.

Για να σας το γράψω πιο απλά, στο καρτεσιανό επίπεδο κάθε σημείο έχει τη μορφή (χ,y) όπου χ= είναι η τετμημένη του στον οριζόντιο άξονα χ’οχ  και  y η τεταγμένη του στον κάθετο άξονα  y’oy  π.χ. ( 1,2). Ο Cramer λοιπόν πήρε 5 τέτοια ζεύγη αντικατέστησε τις ιμές σε κάθε εξίσωση και κατέληξε στο σύστημα.

Το σύστημα μπορεί μεν να το έλυσε αλλά δεν έδωσε τον απαραίτητο λατινικό όρο όπως συνηθιζόταν εκείνη την εποχή.  Ο λατινικός  determinantem όρος προστέθηκε από τον Gauss (1801 )  αλλά είχαμε πέσει σε εποχή που οι μαθηματικοί είχαν μια μικρή ασυνεννοησία γιατί μπορεί μεν ο Gauss να έδωσε όνομα αλλά… δεν εννοούσε αυτό που είχε ο Cramer στο μυαλό του… ( τα γνωστά δηλαδή )

Την υπόθεση ανέλαβε να λύσει ο Cauchy το 1815 ,  o ο οποίος κάνει μια ουσιαστική τομή , τοποθετώντας σε τετραγωνική διάταξη τα στοιχεία της

a11   a12   …… a1n

a21  a22 ……..a2n

………………………

………………………

……………………….

an1  an2 ………. ann

Η ορίζουσα δεν είναι απλά ένας αριθμός , είναι ένας αριθμός που προκύπτει από μια συγκεκριμένη διάταξη π.χ   | 3  2 |

| 7  6 |    δίνει αποτέλεσμα  3*6 – 2 * 7 = 18-14=2

ενώ οι ίδιοι αριθμοί αν διαταχθούν | 2 3|

|7  6 |  δίνει αποτέλεσμα 2*6-3*7 = 12 -21 = -9

Από τη στιγμή που εστιάζουμε στη διάταξη, η ορίζουσα μετονομάζεται σε matrix ( μήτρα ) και αυτή είναι η καταληκτική της ονομασία διεθνώς

Η πρώτη μελέτη της μήτρας γίνεται το 1855 από τον Cayley , ο οποίος προσπαθώντας να  βρει ένα βολικό τρόπο ναεκφράσει εξισώσεις  της μορφής x’=ax+by  & y’=cx+dy κατέληξε σε πίνακες και ορίζουσες και από εκεί στους απαραίτητους μετασχηματισμούς μέσω των πράξεων των πινάκων.

Στους πίνακες ορίζονται οι πράξεις όπως τις ξέρουμε περίπου αλλά με δύο δοαφορές: ο πολλαπλασιασμός πινάκων δεν είναι αντιμεταθετική πράξη όπως γίνεται με τους αριθμούς που όπως και αν τους πολλαπλασιάσεις θα πάρεις το ίδιο αποτέλεσμα και η διαίρεση γίνεται βάσει ορισμού : πολλαπλασιασμός με τον αντίστροφο πίνακα . Αλλά αυτό αρχίζει από εδώ και πέρα και γίνεται μάλλον πολύπλοκο για ένα μπλογκ οπότε καλύτερα ας το αφήσουμε εδώ και ας συνεχίσουμε με το εγκυκλοπαιδικό του πράγματος

πού χρησιμεύουν όλα αυτά;  αφήστε τα , και πού δεν χρησιμεύουν. Πρώτα από όλα ,  ο λογισμός των πινάκων σήμερα είναι μια αυτοτελής μαθηματική θεωρία και εντάσσεται στον κλάδο της Γραμμικής Άλγεβρας.  Η οποία για όσους την έχουμε διδαχθεί στα πρώτα εξάμηνα  των σπουδών μας, παρέχει ένα εργαλείο αρχικά ανάγνωσης, κατανόησης και στη συνέχεια εφαρμογής στο 90% των μελετών μας.

Στοιχεία, αντοχές, υλικά, αποδόσεις, συνθήκες, μοντέλα  στην καταληκτική τους μορφή εμφανίζονται μέσω ενός matrix result. Και όλα αυτά γιατί το 1925 ο Werner Heisenberg

( Physics Nobel Prize ) χρησιμοποίησε τη θεωρία των πινάκων για να εκφράσει τα μη αντιμεταθετικά μαθηματικά που του ήταν απαραίτητα για να εκφάσει τα φαινόμενα της κβαντικής Φυσικής  .. και όλα αυτά επειδή ένας κινέζος είχε κάποτε ένα πρόβλημα με τη σοδειά του σιταριού.. τόσο απλά.

Στο επόμενο τί προτιμάτε; Ένα ταξίδι στους μιγαδικούς ή να γνωρίσετε τις μυστηριώδεις κωνικές τομές;  Αποφασίστε και σας ευχαριστώ για την υπομονή σας, αλλά πρέπει να βγάλουμε και το ψωμί μας

Και ένα κινέζικο πρόβλημα με μεγάλη ιστορία /1

Στο κινέζικο βιβλίο «Εννέα κεφάλαια στη μαθηματική τέχνη» αναφέρεται το εξής πρόβλημα:

3 δεμάτια μιας καλής συγκομιδής, 2 δεμάτια μιας μέτριας συγκομιδής και ένα δεμάτι μιας μέτριας συγκομιδής δίνουν 39 dou σιτάρι.

2 δεμάτια της καλής, 3 της μέτριας και 1 της κακής δίνουν 34  dou σιτάρι

1 δεμάτι της καλής, 2 δεμάτια της μέτριας και 3 δεμάτια της κακής δίνουν 26 dou σιτάρι. Να βρεθεί πόσο σιτάρι δίνει ένα δεμάτι από κάθε είδος συγκομιδής

Το πρόβλημα αυτό ανάγεται σήμερα στην επίλυση ενός γραμμικού συστήματος εξισώσεων με τρεις αγνώστους , όπου χ είναι τα δεμάτια τηα καλής συγκομιδής, ψ είναι τα δεμάτια της μέτριας και z τα δεμάτια της κακής συγκομιδής

Το σύστημα είναι πρωτοβάθμιο και έχει αυτή τη μορφή:

3χ+2ψ+z = 39

2χ+3ψ+z=34

χ+2ψ+3z= 26

Το εντυπωσιακό είναι ότι στο αρχαίο κείμενο δεν υπάρχουν καθόλου σύμβολα, δίνονται οδηγίες για την τοποθέτηση των αριθμών στις κατακόρυφες στήλες ενός άβακα σύμφωνα με τον εξής τρόπο

1      2     3

2     3      2

3     1      1

26  34  39

και με μια σειρά πράξεων που γίνεται μεταξύ γραμμών και στηλών του πίνακα ( στην πραγματικότητα με μετασχηματισμούς που ξανα-ανακαλύφθηκαν μετά από χιλιάδες χρόνια, ) το σύστημα επιλύεται και μας απαντά πώς

1 δεμάτι κακής συγκομιδής δίνει  2.75  dou σιτάρι

1 δεμάτι μέτριας συγκομιδής δίνει 4.25 dou σιτάρι και

1 δεμάτι καλής συγκομιδής δίνει 9.25 dou σιτάρι

Το πρόβλημα αυτό εκφράζεται και επιλύεται τον 3ο αι.  π.Χ. και η ελληνική συμβολή σε αυτό έρχεται από το έργο «Αριθμητικά» του Διόφαντου στην Αλεξανδρινή περίοδο. Χαρακτηριστικό είναι το πρόβλημα αρ. 19 , του οποίου ο τρόπος επίλυσης βρίσκεται πολύ κοντά στο σύγχρονο αλγεβρικό τρόπο σκέψης

Διαβάζουμε: «Ευρείν τέσσαρας αριθμούς όπως οι τρεις λαμβανόμενοι του λοιπόυ υπερέχωσιν επιταχθέντι αριθμό.» Μισό να πέσει και η μετάφραση γιατί τα κινέζικα dou τα καταλάβαινα περισσότερο από αυτό

Να βρεθούν 4 αριθμοί έτσι ώστε λαμβανόμενοι ανά τρεις να ξεπερνούν τον τέταρτο κατά δοθέντα αριθμό)

Ο Διόφαντος δίνει μια πραγματικά σοφιστικέ λύση μέσα από μια ειδική περίπτωση του προβλήματος ( η οποία γενικεύεται άμεσα και δίνει γενική λύση στο πρόβλημα ) ****

Έστω γράφει ότι οι  α,β,γ ξεπερνούν τον δ κατά 20, οι β,γ,δ ξεπερνούν τον α κατά 30, οι γ,δ,α, ξεπερνούν τον β κατά 40 και οι δ,α,β ξεπερνούν τον γ κατά 50. Το πρόβλημα ανάγεται στην επίλυση του γραμμικού συστήματος

α + β + γ= δ+ 20

β + γ + δ = α + 30

γ + δ + α = β + 40

δ + α + β = γ + 50

Ο Διόφαντος που δε χρησιμοποιεί ειδικά σύμβολα για την πρόσθεση και την ισότητα λύνει το πρόβλημα με την εισαγωγή ενός βοηθητικού αγνώστου που εκφράζει το άθροισμα των τεσσάρων ζητουμένων αριθμών

Έστω λοιπόν ότι α+β+γ+δ = 2χ , τότε

α + β + γ= δ+ 20 => α + β + γ + δ = δ + δ + 20 => 2χ = 2δ + 20 => χ = δ + 10 => δ = χ – 10

(Πρόσθεσε και στα δύο μέλη της αρχικής εξίσωσης το δ, για να σχηματίσει το 2χ και να επιλύσει το δ ως προς χ . Η διαδικασία αυτή λέγεται αναγωγή σε ένα άγνωστο και είναι απλά μεγαλοφυιής επινόηση )

β + γ + δ = α + 30 => α + β + γ + δ = α + α + 30 = > 2χ = 2α + 3ο => χ = α + 15 => α = χ – 15

γ + δ + α = β + 40 => β + γ + δ + α = β + β + 40 => 2χ = 2β + 40 => χ = β + 20 => β = χ – 20

δ + α + β = γ + 50 => γ + δ + α + β = γ + γ + 50 => 2χ = 2γ + 50 => χ = γ + 25 => γ = χ – 25

Προσθέτει κατά μέλη τις 4 τελευταίες ισότητες και συνάγει:

α + β + γ + δ = 4χ – 70 => 2χ = 4χ – 70 => -2χ = – 70 => χ = 35

Άρα α = 35 – 15 = 20, β = 35- 20 = 15 , γ = 35 – 25 = 10  & δ= 35 – 10 = 25

**** Πολλές φορές στις επιλύσεις των μαθηματικών επιλέγουμε μια λύση με υποθετικούς αριθμούς όπως εδώ που ο Διόφαντος αυθαίρετα έβαλε τα 20,30,40,50 χωρίς όμως να έχουμε βλάβη της γενικότητας της λύσης. Αυτό συμβαίνει από τις ιδιότητες της διάταξης. Δηλαδή το άθροισμα των πραγματικών είναι πραγματικός αριθμός, συνεπώς από τη στιγμή που η πράξη μπορεί να πραγματοποιηθεί για κάθε πραγματικό αριθμό μπορεί να ισχύσει και για τους συγκεκριμένους .

Και δεν είναι τυχαίο ότι ο Διόφαντος επέλεξε την απόσταση ανά δεκάδα στους αριθμούς, δεδομένου ότι είναι ο κατεξοχήν μαθηματικόςο που εργαζόταν στους φυσικούς , αφήνοντας μας και την περίφημη διοφαντική εξίσωση να πλανιέται ανά τους αιώνες. Το κάνει για να μπορεί να έχει εύρος διαχείρισης στη δεκάδα όπου σίγουρα  έχει άρτιους, περιττούς, 3 πολλαπλάσια του 3 και δύο του πέντε ανά δεκάδα.

Ακολουθεί σιωπή αιώνων, και το πρόβλημα ανασύρεται από τον Leibniz. Mέχρι τότε η Κίνα έχει βγάλει τόσες παραγωγές σταριού ικανές να σιτίσουν κόσμο και κόσμο.

Στις 28.Απριλίου. 1693 ο G.W.Leibniz σε μια επιστολή του στον l’ Hospital , προτείνει μια μέθοδο χρησιμοποίησης των αριθμών για την έκφραση γενικών σχέσεων , όπως ακριβώς γίνεται με τη χρήση γραμμάτων. Έτσι λοιπόν συντάσσει ένα γραμμικό σύστημα 3 εξισώσεων με 2 αγνώστους γραμμένο στην εξής μορφή:

10 + 11 χ + 12 ψ = 0

20 + 21 χ + 22 ψ = 0

30 + 31 χ + 32 ψ = 0

Το περίεργο είναι ότι εδώ οι συντελεστές του συστήματος δηλαδή 11, 12, 21, 22, 31, 32, 10, 20 , 30 δεν εκφράζουν αριθμούς αλλά λειτουργούν όπως οι διπλοί δείκτες εισόδου που χρησιμοποιούνται σήμερα για την παράσταση των στοιχείων ενός πίνακα.

Για να μη σας κουράζω , το πιο χαρακτηριστικό παράδειγμα είναι το Excel όπου κάθε τετραγωνίδιο έχει τον κωδικό ( στήλη, γραμμή ) π.χ. Α1 ( Α στήλη , 1η  γραμμή ). Στα Μαθηματικά που χρησιμοποιούμε εμείς δεν έχουμε τέτοιες πολυτέλειες αυτό το στοιχείο θα το γράφαμε a11 όπου το πρώτο ένα μας υποδεικνύει τη γραμμή  και το δεύτερο 1 τη στήλη

Ο Leibniz ονομάζει αυτούς τους συντελεστές «ψευδοαριθμούς»  και δείχνουν με το πρώτο ψηφίο τους την εξίσωση στην οποία βρίσκονται και με το δεύτερο το γράμμα στο οποίο ανήκουν.  Χρησιμοποιώντας τη μέθοδο των αντίθετων συντελεστών, για να απαλείψει τον ένα από τους δύο αγνώστους , απαλείφει τον άγνωστο ψ αρχικά από την πρώτη και τη δεύτερη εξίσωση και κατόπιν από την πρώτη και την τρίτη. Έτσι του προκύπτουν ισοδύναμες εξισώσεις

10*22 + 11 * 22 χ – 12 * 20 – 12 * 21 χ = 0

10 * 32 + 11 * 32 χ – 12 * 30 – 12 * 31 χ = 0

Από αυτές τις δύο τελευταίες απαλείφει το χ , λύνοντας την καθεμιά ως προς χ και εξισώνοντας τα αποτελέσματα  και φτάνει σε μια ισότητα με πολύ μεγάλη σημασία, τόση ώστε όλοι εμείς που διαχειριζόμαστε συστήματα εξισώσεων να ξέρουμε από την πρώτη ματιά αν το σύστημα έχει λύση.

Για την ιστορία και μόνο του πράγματος, η τελική εξίσωση στην οποία φτάνει ο Leibniz είναι η εξής:

10*21*32 + 11*22*30 + 12 * 20 * 31 – 10*22*31-11*20*32-12*21*30 = 0

Δηλαδή υπολόγισε την ορίζουσα του επαυξημένου πίνακα του συστήματος και δίνει την αναγκαία και ικανή συνθήκη για να έχει επίλυση το σύστημα, η επαυξημένη ορίζουσα θα πρέπει να είναι ίση με το 0.

Ποια είναι η φυσική σημασία των συστημάτων των εξισώσεων;

Στα γραμμικά πρωτοβάθμια συστήματα, οι εξισώσεις παριστούν ευθείες. Όταν το σύστημα έχει λύση οι ευθείες τέμνονται, όταν το σύστημα δεν έχει λύση ( αδύνατο σύστημα ) οι ευθείες είναι παράλληλες και όταν το σύστημα είναι αόριστο ( δηλαδή ικανοποιείται από οποιοδήποτε χ και ψ ) τότε οι ευθείες ταυτίζονται.

Συνεχίζεται

Η μαθηματική επαγωγή και ο κύριος Bernoulli

ή διαφορετικά η μαθηματική επαγωγή στις ανισότητες < ανισότητα  Βernoulli >

Να αποδειχθεί ότι γι α κάθε ακέραιο αριθμό ν≥2 και για κάθε πραγματικό αριθμό α , με α <>0 και α>-1 ισχύει:

(1+α)^ν > 1 + να

Απόδειξη: Ξεκινάμε την απόδειξη για  ν=2 ( λόγω του περιορισμού )

(1+α)² = 1 + 2•α + α² > 1 + 2•α <=> α² > 0( σχέση που ισχύει για κάθε πραγματικό αριθμό  α )

<!– @page { margin: 0.79in } P { margin-bottom: 0.08in } –>

[ Τί κάναμε εδώ; υψώσαμε το (1+α) στο τετράγωνο, χρησιμοποιώντας τη γνωστή ταυτότητα , χρησιμοποιήσαμε την ανισότητα, ξέροντας ότι έχουμε να κάνουμε με θετικές ποσότητες διαγράψαμε από τα δύο μέλη της ανισότητας τις ίδιες ποσότητες και καταλήξαμε ότι το α² > 0 που ισχύει για κάθε πραγματικό αριθμό α

Συνεχίζουμε δεχόμενοι ότι η ανισότητα ισχύει για τον τυχαίο θετικό ακέραιο ν :

ν=κ (1+α)^κ > 1 + κ•α

Και συνεχίζουμε να αποδείξουμε ότι ισχύει και για τον επόμενό του τον ν=κ+1

Για ν=κ+1 θα ισχύει  :                  (1+α)^κ+1 > 1 +(κ+1)•α

Απόδειξη:

(1+α)^κ+1 = (1+α)^κ * (1+ α) ( ιδιότητες δυνάμεων )> (1+ κα) * (1+ α ) όπου

(1+ κα) * (1+ α ) =  1 + κ•α + α + κ•α² ( χρήση επιμεριστικής ιδιότητας ) =

1+ (κ+1)•α ( παραγοντοποίηση ) + κ•α² > 1 +(κ+1) •α

Γνωριμία με τον κύριο Bernoulli

O Daniel Bernoulli, Δανο-Σουηδικής καταγωγής, μεγάλωσε σε ένα οικογενειακό περιβάλλον που τα μαθηματικά ήταν κυρίαρχα. Αυτό είχε σαν αποτέλεσμα προφανώς να καλλιεργηθεί ακόμα περισσότερο το έμφυτο ταλέντο του και όχι μόνο να παραδώσει εργασίες που αφορούσαν τα μαθηματικά αλλά να προεκτείνει τις μελέτες του τόσο στη μηχανική ρευστών και το πιο καταπληκτικό στη Στατιστική μελέτη ( που σίγουρα κανείς δεν υποψιαζόταν την ύπαρξή της μεταξύ 1700 και 1782 που έζησε ο Bernoulli ( εκτός από τον ίδιο φυσικά )

Like father like son … αν και ο πατέρας του γνωρίζοντας ότι η οικονομική επιτυχία  ενός μαθηματικού ήταν αβέβαιη τον παρότρυνε να σπουδάσει οικονομικά ο D.Bernoulli κάνοντας έναν επιστημονικό κύκλο από το Business administration περνώντας στην ιατρική καταλήγει στα μαθηματικά τα οποία δεν ολοκληρώνει σε πανεπιστημιακό επίπεδο αλλά ολοκληρώνει διδασκόμενος από τον πατέρα του ( για την ακρίβεια η παραχώρηση για να σπουδάσει ιατρική περιείχε μια συμφωνία κυρίων ανάμεσά τους )

Οι μαθηματικές εργασίες του Bernoulli «συγχορδίζονται» και επεκτείνουν στη μηχανική πολλές από τις εργασίες των  Euler, Goldbach, MacLaurin, Laplace, Taylor, D’ Alembert  ( και μην απορείτε που τους ξέρουμε με τα ονοματά τους, τα θεωρήματα και οι αρχές είναι κωδικοποιημένες οπτικά πια μέσα «βιβλιοθήκη» που κουβαλάει μέσα του και ένας μηχανικός και ένας μαθηματικός )

Οι μαθηματικές  αναπτύξεις   Bernoulli στην συμπεριφορά των αερίων εξηγούν το νόμο του Boyle και αποτελούν βασική αρχή στη θεωρία της θερμοδυναμικής.

Εκεί που πραγματικά όμως γίνεται η επανάσταση , είναι όταν ο Bernoulli μιλά πρώτος

για ρίσκο και επιχειρεί την πρώτη στην ιστορία  risk analysis , το 1738  , δηλαδή επιχειρεί να δημιουργησει και το πετυχαίνει στοχαστικό μοντέλο πρόβλεψης

Μας δίνει την κατανομή Bernoulli ( στην ουσία μια συνάρτηση που περιγράφει ένα στατιστικό δείγμα και ισχύει ακόμα ως ισχυρό εργαλείο  ) μελετώντας την επικινδυνότητα της ευλογιάς στους πληθυσμούς  και τη αξία του εμβολιασμού .

Μαθηματική επαγωγή / 1

Στους συλλογισμούς που κάνουμε σε καθημερινό επίπεδο η επαγωγή χρησιμοποιείται συνήθως για να τους γενικεύσει .

Ένα παράδειγμα είναι: η γενικευμένη οικονομική κρίση δημιουργεί ανέργους συνεπώς κάθε εργαζόμενος είναι εν δυνάμει άνεργος στο άμεσο μέλλον.Αυτή είναι μια μάλλον «ασφαλής» γενίκευση αν και στην παραπάνω πρόταση ο επαγωγικός λογισμός ενισχύει το συμπέρασμα αλλά δεν το αποδεικνύει.

Συχνό παράδειγμα επαγωγής είναι οι διατυπώσεις στα δελτία ειδήσεων ή τα πρωτοσέλιδα των εφημερίδων όπως:

Παρατηρείται αλματώδης αύξηση της εγκληματικότητας ,άρα  η Αθήνα έγινε Μπογκοτά ή Μανίλα

Αλλά και εκφράσεις όπως ο πάγος είναι κρύος άρα δεν υπάρχει πάγος στον ήλιο

Οι παραπάνω εκφράσεις είναι εισαγωγικές για να αντιληφθούμε την ισχύ και λειτουργία της επαγωγής άλλοτε επιτυχημένα και άλλοτε όχι, στους καθημερινούς συλλογισμούς.

Μια άλλη  μορφή  της επαγωγής,   είναι όταν  χρησιμοπιοιείται για να εξάγει συμπεράσματα για το μέλλον χρησιμοποιώντας την εμπειρία του παρελθόντος ή ενός μικρού συστήματος μελέτης

όπως : Αν παρατηρήσουμε το δικό μας γαλαξία μπορούμε να εξάγουμε αποτέλεσμα για το σύμπαν, αν εκτιμήσουμε μια τοπική οικονομία μπορούμε να εξάγουμε συμπεράσματα για το εθνικό σύστημα

Η επαγωγή όμως στα Μαθηματικά και τη Φυσική έχει μια εντελώς διαφορετική λειτουργία.

Στα μεν μαθηματικά αποτελεί μια ισχυρότατη απόδειξη , στη δε φυσική έχει άμεση σχέση με τις ηλεκτρικές δυνάμεις που αναπτύσσονται από απόσταση ή εξαιτίας του ηλεκτρομαγνητικού πεδίου

Ποια είναι ακριβώς η επαγωγή στα μαθηματικά;

Η επαγωγή στα Μαθηματικά είναι η  απόδειξη που στηρίζεται στην αρχή της καλής διάταξης στους φυσικούς αριθμούς

Σύμφωνα με την αρχή της καλής διάταξης ή αρχή του ελαχίστου , όλα τα μη κενά υποσύνολα φυσικών αριθμών περιέχουν ένα στοιχείο που είναι ελάχιστο.

Με άλλα λόγια αν S είναι ένα μη κενό υποσύνολο του Ν, τότε υπάρχει ένα στοιχείο τέτοιο ώστε για κάθε στοιχείο να ισχύει s ≤ α.

Δηλαδή δεν υπάρχει περίπτωση στους φυσικούς αριθμούς να επιλέξουμε ένα υποσύνολο και μέσα σε αυτό να μην υπάρχει το μικρότερο στοιχείο , ακόμα και αν κινούμαστε στις περιοχές κοντά στο άπειρο.

Περιγραφή της μεθόδου

Έστω ότι πρόκειται να αποδειχθεί μια πρόταση

Αποδεικνύουμε την ισχύ της πρότασης για τον μικρότερο φυσικό αριθμό ( βήμα 1 )

Αποδεχόμαστε την την ισχύ της Ρ(ν) για ν = κ  ( βήμα 2 ) και

Αποδεικνύουμε την ισχύ της Ρ(ν+1) , δηλαδή για τον επόμενο φυσικό αριθμό του ν ( βήμα 3 )

Παράδειγμα 1:

Να αποδειχθεί ότι για κάθε φυσικό αριθμό ν, ισχύει:

1²+2²+3²+….+ν² = ν*(ν+1)*(2*ν+1)/6 ( εδώ υπολογίζουμε το άθροισμα των τετραγώνων των φυσικών αριθμών )

Για ν=1 θα έχουμε 1² = 1*(1+1)*(2*1+1)/6=1*2*3/6 = 6/6 = 1 (1) ( που ισχύει )

Αποδεχόμαστε την Ρ(ν) => 1²+2²+3²+….+ν² = ν*(ν+1)*(2*ν+1)/6 (2)

Θα αποδείξουμε την Ρ(ν+1)

Ρ(ν+1) = 1²+2²+3²+….+ν² + (ν+1)² = (ν+1)*(ν+2)*[2*(ν+1)+1]/6

( στο πρώτο μέλος -αριτερά του ίσον δλδ  προσθέτουμε το (ν+1)² και στο δεύτερο μέλος όπου στην προηγούμενη πρόταση είχαμε ν θέτουμε ν+1 )

και μετά από πράξεις γίνεται

Ρ(ν+1) = 1²+2²+3²+….+ν² + (ν+1)² = (ν+1)*(ν+2)*(2*ν+3) / 6

Απόδειξη:

Ρ(ν+1) = 1²+2²+3²+….+ν² + (ν+1)² = ν*(ν+1)(2*ν+1)/6 + (ν+1)² =

(αντικατάσταση του αθροίσματος από τη σχέση (2)

(ν+1) * [ ν*(2*ν + 1) / 6 + (ν+1) ]

( εξαγωγή κοινού παράγοντα (ν+1)

(ν+1) * [ν* (2*ν+1) + 6* (ν+1)]/6

( ομώνυμα κλάσματα )

(ν+1) * ( 2*ν ² + 7 * ν + 6 )/ 6

(παραγοντοποίηση του τριωνύμου 2*ν ² + 7 * ν + 6 ( με χρήση διακρίνουσας κλπ – για να μη σας κουράζω και άλλο )

(ν+1)*(ν+2)*(2*ν+3)/6

Αποδείξαμε λοιπόν ότι η Ρ(ν+1) είναι αληθής άρα η αρχική μας υπόθεση ισχύει για όλους τους φυσικούς αριθμούς

Στη μαθηματική επαγωγή αφήνουμε συνήθως να μας οδηγήσει η απόδειξη οπως σε αυτό το παράδειγμα , χωρίς να ξεχνάμε ότι μπορεί σε οποιοδήποτε στάδιο να μας ζητηθεί ακόμα και η πιο απίθανη πρόταση, μέθοδος της Άλγεβρας

Στο επόμενο η μαθηματική επαγωγή στις ανισότητες

ΥΓ

Να βάλω ασκήσεις;

Ιστορικό σημείωμα/1

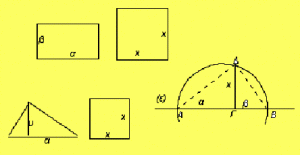Ο «διπλασιασμόςτου τετραγώνου» δηλαδή η κατασκευή ενός τετραγώνου με εμβαδό διπλάσιο ενός άλλου δοθέντος τετραγώνου , μπορεί να γίνει με μια απλή «γεωμετρική κατασκευή», δηλαδή με κανόνα και διαβήτη

Ωστόσο η πλευρά  β , του τετραγώνου με το διπλάσιο εμβαδό δεν προκύπτει από την πλευρά α με πολλαπλασιασμό επί  ρητό αριθμό. Αυτό σημαίνει ότι δεν υπάρχει ευθύγραμμο τμήμα ( ως μονάδα μέτρησης ) με το οποίο μπορούμε να μετρήσουμε ακριβώς τα δύο αυτά τμήματα , πλευρά και διαγώνιο τετραγώνου.

Δηλαδή με απλά λόγια: το εμαβαδόν τετραγώνου πλευράς α , δίνεται από τη σχέση Ε=α↑2, δηλαδή ένα τετράγωνο με πλευρά α=2 cm, θα έχει εμβαδό Ε= 2*2 = 4 cm↑2.

H διαπίστωση είναι ότι αν θέλουμε ένα τετράγωνο με Ε= 8 cm↑2, αυτό δεν θα μας προκύψει αν πάρουμε το προηγούμενο τετράγωνο με την πλευρά των 2 cm και διπλασιάσουμε την πλευρά του, γιατί σε περίπτωση που το κάνουμε αυτό το τετράγωνο που θα προκύψει θα είναι εμβαδού 16 cm↑2

Η απόδειξη της ύπαρξης άρρητων αριθμών θεωρείται μια από τις σπουδαιότερες ανακαλύψεις των Πυθαγορείων.

Οι αρχαίοι Έλληνες πίστευαν ότι πάντοτε δύο ευθύγραμμα τμήματα έχουν κοινό μέτρο. Γι’ αυτό στα πλαίσια της εποχής εκείνης , η ανακάλυψη αυτή των Πυθαγορείων δεν ήταν απλά και μόνο μια ενδιαφέρουσα μαθηματική πρόταση αλλά εσήμαινε την ανατροπή θεμελιωδών φιλοσοφικών αντιλήψεων για τον κόσμο και τη φύση.

Ήταν κεντρική αντίληψη των Πυθαγορείων ότι η ουσία κάθε όντος μπορεί να αναχθεί σε φυσικούς αριθμούς.  Ο νεοπυθαγόρειος Φιλόλαος έγραψε: Πραγματικά το κάθε τι που γνωρίζουμε έχει έναν αριθμό. Αλλοιώς θα ήταν αδύνατο να το γνωρίσουμε και να το καταλάβουμε με τη λογική. Το Ένα είναι η αρχή του παντός.

Η ανακάλυψη λοιπόν ότι υπάρχουν μεγέθη και μάλιστα απλά όπως η υποτείνουσα τετραγώνουν τα οποία δεν μπορούν να εκφραστούν στα πλαίσια των φυσικών αριθμών , θεωρήθηκε αληθινή συμφορά για την πυθαγόρεια φιλοσοφία.

Χαρακτηριστικά αναφέρεται , ότι η ανακάλυψη αυτή έγινε από τον Πυθαγόρειο Ίππασο όταν οι υπόλοιποι Πυθαγόρειοι ταξίδευαν με πλοίο.  Η αντίδραση των Πυθαγορείων ήταν ν απνίξουν τον Ίππασο και να συμφωνήσουν μεταξύ τους να μη διαδοθεί η ανακάλυψη προς τα έξω.

Η υπέρβαση των δυσκολιών που φέρνει στα μαθηματικά η ύπαρξη άρρητων αριθμών κατέστη δυνατή από τον Εύδοξο με την ιδιοφυή θεωρία των  «Λόγων»

Η απόδειξη ότι ένας αριθμός είναι άρρητος είνα ένα πρόβλημα που πολλές φορές απαιτεί πολύπλοκους συλλογισμούς.

Μια απόδειξη όμως για το γεγονός ότι ο √2 είναι άρρητος γίνεται με την μέθοδο της «απαγωγής σε άτοπο»

Έστω ότι ο √2 είναι ρητός, τότε √2=κ/λ , όπου κ και λ είναι φυσικοί αριθμοί και το κ/λ είναι ανάγωγο κλάσμα ( έχουν γίνει δηλαδή όλες οι δυνατές απλοποιήσεις )

Τότε θα ισχύει √2= κ/λ ↔

(√2)↑2 = (κ/λ)↑2

↔2 = κ↑2/λ↑2

↔κ↑2=2*λ↑2 που  που σημαίνει ότι ο κ↑2 είναι άρτιος.

Αν όμως ο κ↑2 είναι άρτιος ↔ υπάρχει μοναδικός φυσικός μ τέτοιος ώστε:

(2*μ)↑2 = 2*λ↑2 ↔ 4*μ↑2=2*λ↑2  ↔ λ↑2=2*μ↑2

που σημαίνει ότι και ο λ↑2 είναι άρτιος, άρα και ο λ είναι άρτιος.

Αφού λοιπόν καταλήγουμε ότι οι κ και λ είναι άρτιοι, τότε το κλάσμα κ/λ δεν είναι ανάγωγο. Αυτό το τελευταίο είναι άτοπο.

Γενικά αποδεικνύεται ο √ν είναι άρρητος αριθμός, όταν ο ν δεν είναι τετράγωνο φυσικού αριθμού.

ΥΓ Πραγματικά ο WordPress editor έχει δυνατότητες αλλά ας έβαζε και τη συνεπαγωγή για να μη χρησιμοποιώ το ↔, στη θέση της

H διάταξη των αριθμών

Οι αριθμοί διατάσσονται στην ευθεία των πραγματικών αριθμών. Φαντασθείτε αυτή την ευθεία ως ατελείωτη γεμάτη αριθμούς, που ξεκινά από το -άπειρο ( -00) , φτάνει στο + άπειρο (+00)

Η υπόθεση της διάταξης είναι θεμελιώδης για την κατανόηδη της Άλγεβρας, όταν αυτή ξεφεύγει από τον υπολογιστικό της χαρακτήρα.

Ας πάρουμε δύο θετικούς αριθμούς. Έχουμε μάθει ότι το 3 < 4 και όσο μεγαλώνουν οι αριθμοί η ανισότητα αυτή παραμένει σταθερή.

Όμως το 1/3 >1/4  πράγμα που είναι φυσιολογικό Δεν είναι το ίδιο να μοιράσεις κάτι στα 3 από ότι στα 4.

Μαθαίνουμε λοιπόν ότι αν χ1<χ2  –> 1⁄χ1 >1⁄χ2

Το σημαντικότερο σημείο είναι η συμπεριφορά στη διάταξη των αρνητικών αριθμών. Εδώ για την κατανόηση παίζει μεγάλο ρόλο η αντίληψη της απόλυτης τιμής, δηλαδή της απόστασης ενός αρνητικού από το σημείο 0.

Όσο πιο μακριά βρίσκεται ο αριθμός από το 0, τόσο πιο μικρός είναι. Έτσι λοιπόν το -1000 είναι μικρότερο από το -0.00001 , ακριβώς γιατί το δεύτερο βρίσκεται σε απόσταση αναπνοής από το 0 ( ή τουλάχιστον έτσι θέλουμε να πιστεύουμε ).

Φυσικά η ανισοτική σχέση αντιστρέφεται όταν οι αριθμοί γίνουν κλάσματα όπως και στους θετικούς αριθμούς.

Καταλαβαίνουμε λοιπόν ότι σε μια ανισοτική σχέση είτε στους θετικούς είτε στους αρνητικούς όταν ο μεγαλύτερος γίνει παρονομαστής του κλάσματος παράγει μικρότερο κλάσμα από κάθε μικρότερό του αριθμό.

Αυτό όσο και αν φαίνεται απλοϊκό και ευκολονόητο ( και είναι ) είναι ένα τέχνασμα που δύσκολα έρχεται στο μυαλό στις αποδείξεις των ανισοτικών σχέσεων.

Αν ξεπεραστεί αυτό το θέμα, τότε έρχονται πιο ομαλά οι υπόλοιπες ιδιότητες των ανισοτήτων, για παράδειγμα μια αριθμητική ανισότητα δεν αλλάζει φορά αν της προσθέσουμε ή της αφαιρέσουμε τον ίδιο αριθμό ή αν την πολλαπλασιάσουμε ή διαιρέσουμε με ένα θετικό αριθμό.

Είτε αυτό συμβεί στους θετικούς είτε στους αρνητικούς αριθμούς.

Θα σταθούμε όμως στον πολλαπλασιασμό: όταν πολλαπλασιάζουμε με αρνητικό αριθμό η ανισότητα αλλάζει φορά. Το ίδιο και αν διαιρέσουμε ( εξάλλου και η διαίρεση είναι ένας πολλαπλασιασμός )

Οι αριθμοί όπως διαπιστώνουμε έχουν μια συμμετρία και υπακούουν σε κανόνες που δεν είναι αφηρημένοι. Μια συχνή μαθηματική συζήτηση είναι αν στα πεδία επέκτασης της μελέτης των αριθμών, μιλάμε για ρεαλιστικές συμπεριφορές ή για απλές υποθέσεις. Η μελέτη θα δείξει

Numbers

Οι πρώτοι, είναι οι φυσικοί, γνωστοί και ως Ν από τη λατινική λέξη Natura. Οι αριθμοί της καθημερινότητάς μας, αυτοί που μπορούμε να αντιληφθούμε καλύτερα.

Στη συνέχεια, η επέκταση στους ακεραίους, οι αριθμοί που χρειάστηκε να επινοηθούν για να δικαιολογηθούν διάφορες φυσικές παρατηρήσεις όπως θερμοκρασίες κάτω από το μηδέν. Σύμβολό τους το Ζ.  Μόνο που ο κόσμος δεν είναι ακέραιος. Αρνητικοί και θετικοί αλλά ρητοί, δηλαδή κλασματικοί. Αλήθεια και ποιοι δεν είναι κλασματικοί; αφού κάθε αριθμός μπορεί να γραφεί με τη μορφή κ/λ …

Σύμβολό τους το Q

To σύνολο μεγαλώνει …

Στη συνέχεια οι άρρητοι, αυτοί που μόνο με προσέγγιση μπορούν να υπολογιστούν. Αλήθεια πόσα ψηφία προσεγγίζουν καλύτερα την τετραγωνική ρίζα του 2, του 3, του 5;

Το σύνολο ολκληρώνεται στη ρεαλιστική του μορφή και όλοι μαζί, φυσικοί, ακέραιοι, ρητοί και άρρητοι είναι τα υποσύνολα των πραγματικών αριθμών R

Mόνο που η φαντασία των μαθηματικών ταξιδεύει διαρκώς, και δημιουργεί τους φανταστικούς αριθμούς, θα ήταν αδιανόητο για μια τέτοια επιστήμη να σταματήσει στο ότι δεν μπορεί να ορίσει την τετραγωνική ρίζα των αρνητικών αριθμών. Με τη χρήση του i γίνεται η υπερπήδηση του εμποδίου και ιδού ο φανταστικός άξονας με άπειρες εφαρμογές στην πραγματικότητα.

Για πολλούς τα μαθηματικά είναι η κορωνίδα των επιστημών, όχι άδικα.

Δε μένει παρά να τα ανακαλύψουμε σταδιακά , ξεκινώντας από το πιο απλό σύνθετο, τη διάταξη στους αριθμούς και φυσικά τις προεκτάσεις της, στο επόμενο επεισόδιο φυσικά

Αποκωδικοποιώντας μια γνωστή άγνωστη γλώσσα

Αποκωδικοποιώντας μια γνωστή – άγνωστη γλώσσα

1. Η πρώτη σκέψη ήρθε ξαφνικά και η δεύτερη ήταν «γιατί όχι»;  Στα blogs γράφονται διάφορα χρηστικά επιστημονικά αλλά δεν αποσαφηνίζονται τα απλά και εύκολα, η βάση δηλαδή.
2. «Μαθηματικά σε απλά μαθήματα», ιδέες δηλαδή
3. Από την τρελή ιδέα ότι η επιστήμη στη βάση της είναι ελεύθερη για όλους.
4. Ελπίζουμε να μας διαβάζετε και να  μας προτείνετε θέματα να σας αναλύσουμε. Δεν υποσχόμαστε ότι θα είμαστε τόσο τακτικοί στις αναρτήσεις μας,
5. ίσως γιατί θέλουμε να είμαστε ακριβείς απλοί και λιτοί , κατανοητοί δηλαδή
6. Θα δείξει πώς θα πάει

Hello world!

Welcome to WordPress.com. This is your first post. Edit or delete it and start blogging!